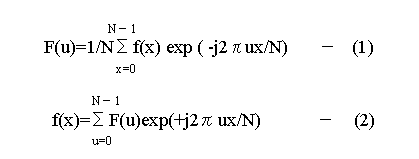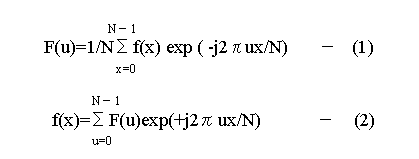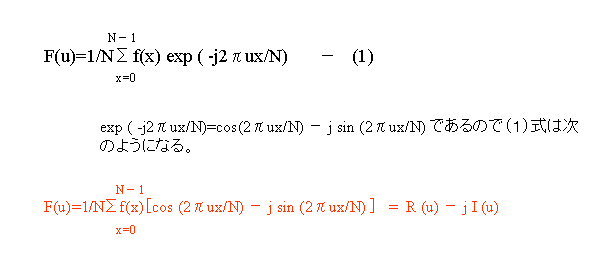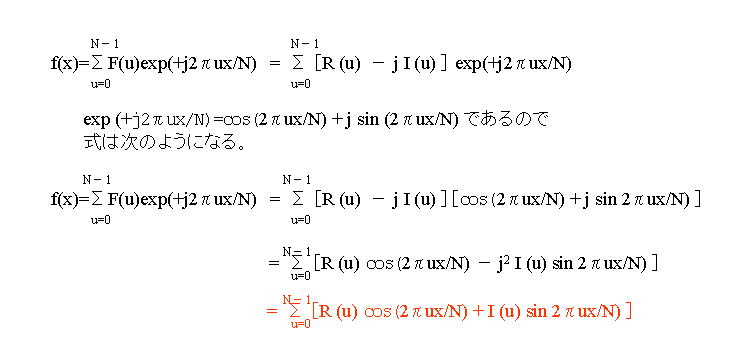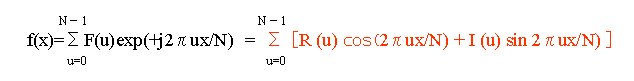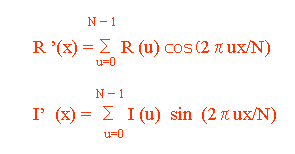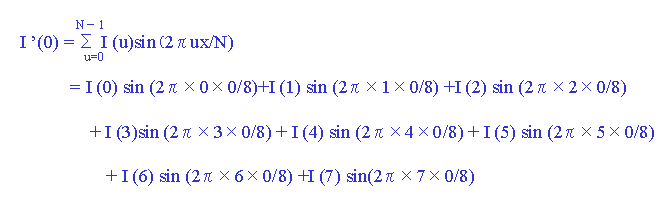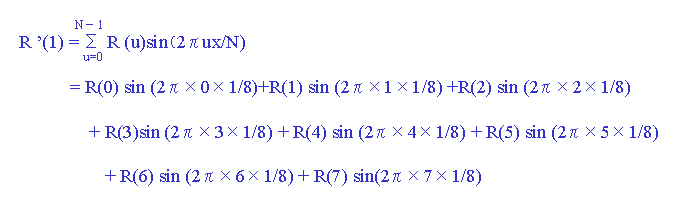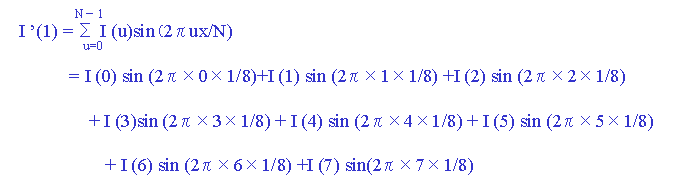離散逆フーリエ変換の基礎（２）

式を考えてみる

再度、離散フーリエ変換（１）の式と離散逆フーリエ変換の式（２）を登場 させてみます。

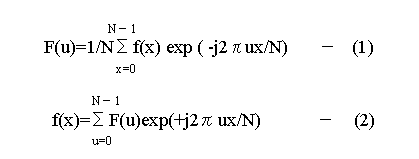
この（１）式を変形させると

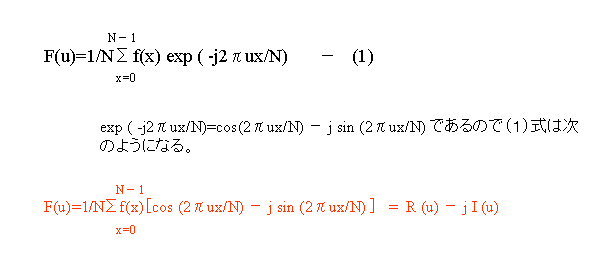
この式（赤）を（２）式に代入させます。
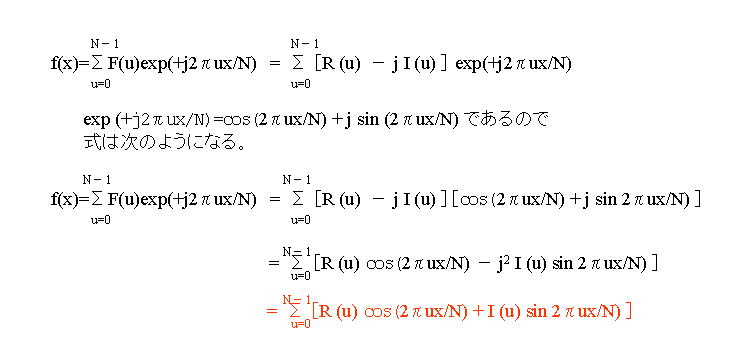これによって、離散逆フーリエ変換が出来たことになります。

この式でははっきりわからない・・・

この式を実際に利用して解いていきましょう。簡単に説明するために、８画素を例にして考えます。
もう一度式を登場させます。

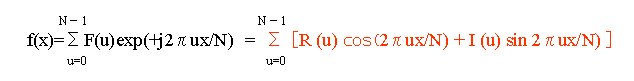
この式に記号は、離散フーリエ変換で説明したものと同じですので説明は省略します。

はじめに、離散フーリエ変換と同じようにcos 頁と sinx 頁に別けて考えます。


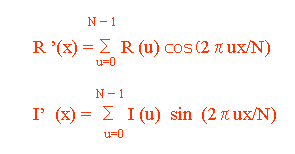
1. x = 0　のときの　cos頁:R'(0)、sin 頁:I'(0)を計算します。




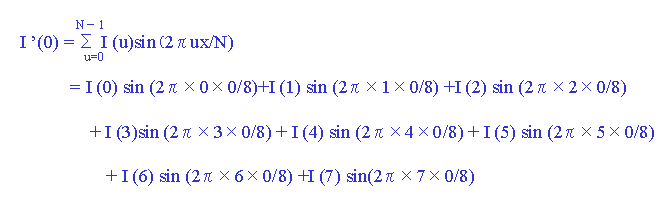
2. x = 1　のときの　cos頁:R'(1)、sin 頁:I'(1)を計算します。




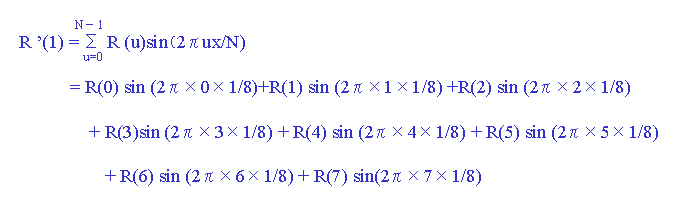
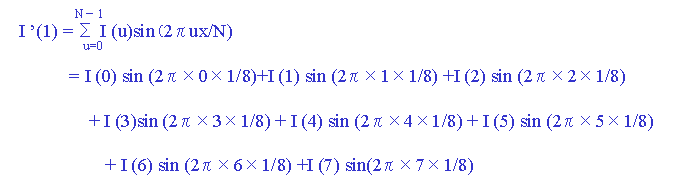
同様にしてｘ＝７　までのR'(ｘ)、I'(ｘ)を全て計算します。
3.　x = 0　のときの　R'(0)　+　I'(0)が離散逆フーリエ変換されたｘ＝０の値となります。
4.　x = 1　のときの　R'(1)　+　I'(1)が離散逆フーリエ変換されたｘ＝１の値となります。
　　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　　・
5.　x = 6　のときの　R'(6)　+　I'(6)が離散逆フーリエ変換されたｘ＝０の値となります。
6.　x = 7　のときの　R'(7)　+　I'(7)が離散逆フーリエ変換されたｘ＝７の値となります。


これで離散逆フーリエ変換ができたことになります。

このことから、離散逆フーリエ変換には｜F(u)|ではなくF(u)が必要なことが理解できたことと思い ます。