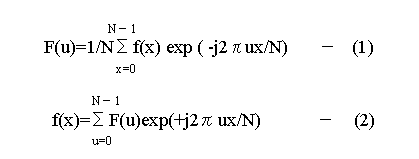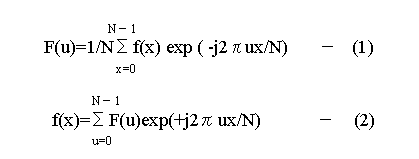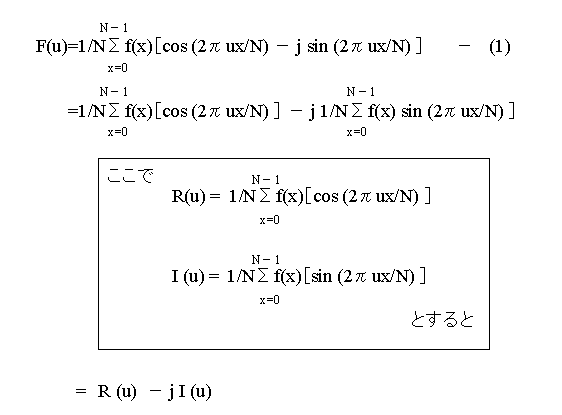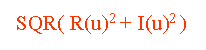離散逆フーリエ変換の基礎（１）

離散逆フーリエ変換とは

前項で離散フーリエ変換について説明しました。
実空間でのフィルタ（例えば、１，２，１）を周波数空間での表現するには離散フーリエ変換を行えば良いことを学びました。
空間周波数表示で示されているフィルタは実空間ではどのようになるのか？の答えを出すのが離散逆フーリエ変換にあたります。

離散逆フーリエ変換は、空間周波数表示を実空間表示に戻す方法となります。

離散フーリエ変換と離散逆フーリエ変換

はじめに、離散フーリエ変換と離散逆フーリエ変換の式を比較してみます。
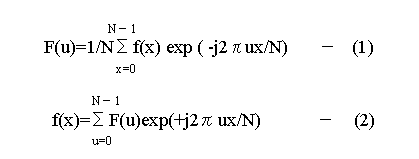　 （１）の式は離散フーリエ変換、（２）の式は離散逆フーリエ変換を示しています。

つぎに、（１）式をもう少し分解してみます。

（１）式のexp(-j2πux/N)は
exp(-j2πux/N) = cos(2πux/N) −　j sin(2πux/N)
　 に変えることができるそうなので、この変形したものを（１）式に代入します。そうすると（１）式 は
　
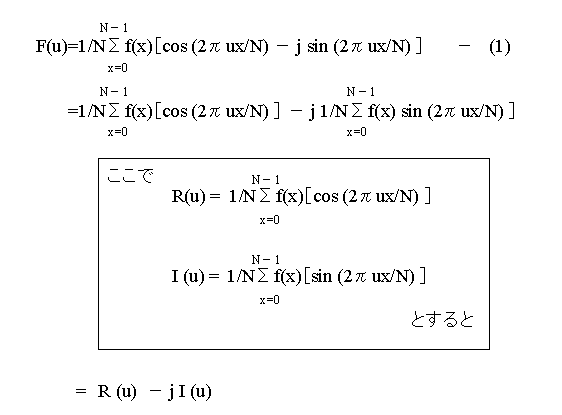
　 となります。このことは離散フーリエ変換の項でも学びました。

　 周波数特性では「何を？」調べたのか

実空間の表現を周波数空間に変化させるのには離散フーリエ変換を行いました。この離散フーリエ変換 で得られた値　R(u) と　I(u) から
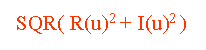
を計算しましたが、これは
F(u)ではなく｜F(u)｜（絶対値）
を導き出していました。

離散逆フーリエ変換の式（２）は
｜F(u)｜ではなくF(u)

が使用してあるので、特性として示されている｜F(u)｜を使うことはできません。では、Butterworth フィルタのように、はじめから周波数特性｜F(u)｜で示されているものを実空間表現に変えるにはどう したら良いのかを考えていきます。
離散逆フーリエ変換には｜F(u)｜ではなくF(u)が必要となるのです。