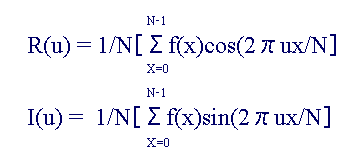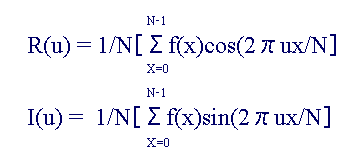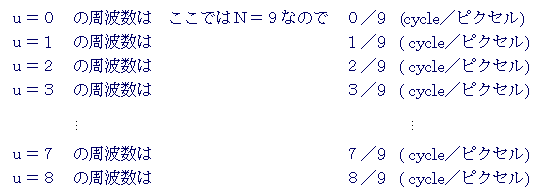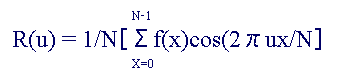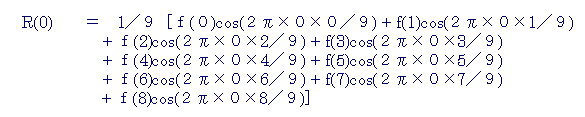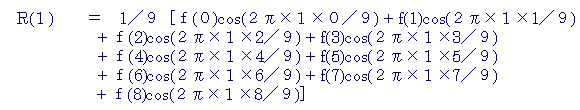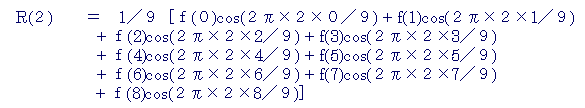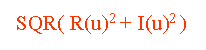棧嶶僼乕儕僄曄姺偺婎慴乮俀乯
們倧倱攇宍偺棧嶶僼乕儕僄曄姺傪偟偰傒傛偆丒丒丒偦偺俀
侾丏偼偠傔偵丄俀偮偺幃傪弨旛偟傑偡丅
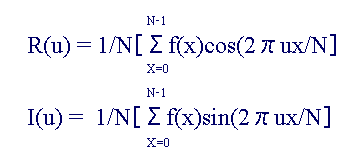 丂
偙偺幃偺塃曈偺俶偼僺僋僙儖偺屄悢偱偡丅
丂
偙偺幃偺塃曈偺俶偼僺僋僙儖偺屄悢偱偡丅
丂丂乮偙偙偱偼俋僺僋僙儖側偺偱俶偼俋偲側傝傑偡丅乯
俀丏倳偼廃攇悢偺斣崋偱丄廃攇悢偱偼偁傝傑偣傫丅偙偺斣崋傕侽偐傜偼偠傑傝
傑偡丅
倳亖侽偲偼0斣栚偺廃攇悢傪堄枴偟傑偡丅倳亖侾偼侾斣栚偺廃攇悢偺偙偲偱偡丅
倳偺廃攇悢偼乮倳偺斣崋乯乛俶偲側傝傑偡丅
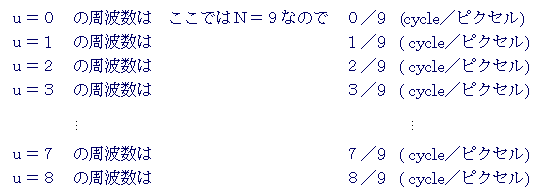 偙傟偱偡傋偰偺婰崋偺堄枴偑棟夝偱偒傑偟偨偺偱R(u)偺幃偵戙擖偟偰偄偒傑偡丅
偙傟偱偡傋偰偺婰崋偺堄枴偑棟夝偱偒傑偟偨偺偱R(u)偺幃偵戙擖偟偰偄偒傑偡丅
幃偼師偺傛偆偵側傝傑偡丅
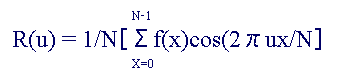 ( N=俋 丄u偼侽偐傜俉傑偱丄倶傕侽偐傜俉傑偱)
( N=俋 丄u偼侽偐傜俉傑偱丄倶傕侽偐傜俉傑偱)
廃攇悢u=侽斣栚丂廃攇悢偱偼侽乛9偺R(u)偼
乮倳亖侽丄俶亖俋丂倶偼曄悢偱侽乣俉乯
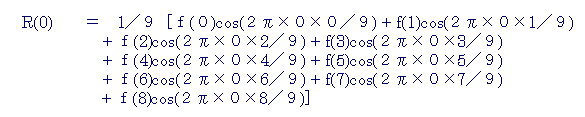 廃攇悢u亖侾斣栚丂廃攇悢偱偼侾乛9偺R(u)偼
廃攇悢u亖侾斣栚丂廃攇悢偱偼侾乛9偺R(u)偼
丂乮倳亖侾丄俶亖俋丂倶偼曄悢偱侽乣俉乯
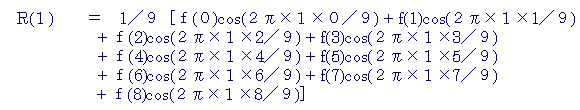 廃攇悢u亖俀斣栚丂廃攇悢偱偼俀乛俋偺R(u)偼
廃攇悢u亖俀斣栚丂廃攇悢偱偼俀乛俋偺R(u)偼
丂乮倳亖俀丄俶亖俋丂倶偼曄悢偱侽乣俉乯
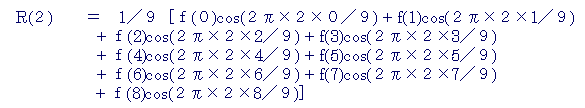
偙偺傛偆偵倳亖俉斣栚傑偱寁嶼偟偰傒偰偔偩偝偄丅俤倶們倕倢偱寁嶼偟偨傜娙扨偱偡丅
俁丏 摨偠傛偆偵俬(u)傕寁嶼偟傑偡丅
係丏 寁嶼偝傟偨R(倳)丄俬(u)偐傜
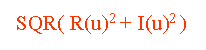 乮SQR偲偼併偺偙偲偱偡丅乯傪寁嶼偟傑偡丅 丂丂丂丂丂丂丂丂丂
乮SQR偲偼併偺偙偲偱偡丅乯傪寁嶼偟傑偡丅 丂丂丂丂丂丂丂丂丂
俆丏 墶幉偵u亖侽偺偲偒偺廃攇悢乮侽乛俋乯丄u亖侾偺偲偒偺廃攇悢乮侾乛俋乯丄u亖俀偺偲偒偺廃攇悢乮俀乛俋乯乣
u亖俈偺偲偒偺廃攇悢乮俈乛俋乯丂丂丂u亖俉偺偲偒偺廃攇悢乮俉乛俋乯傪庢傝丄偦傟偧傟偺廃攇悢偵偍偗傞SQR乮R(倳)俀+俬(u)俀乯偺抣傪僾儘僢僩偡傞偲廃攇悢摿惈偑媮傑傝傑丂丂丂丂偡丅
俇丏 寢壥

偙偺摿惈偼壓偵帵偡傛偆側嘆傗嘇偺傛偆側僇乕僽傪帵偡廃攇悢摿惈偱偼側偔
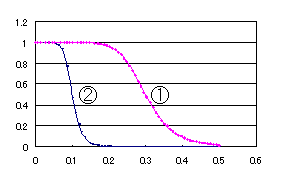
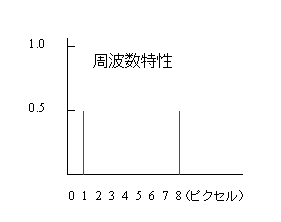 廃攇悢1/9偲8/9偵怳暆乮愨懳抣乯0.5傪傕偮摿惈偲側偭偰偄傑偡丅廃攇悢摿惈偼僇乕僽偱帵偝傟傞傕偺偱偩偗偱偼側偄偙偲傪偍傏偊偰偍偄偰偔偩偝偄丅
廃攇悢1/9偲8/9偵怳暆乮愨懳抣乯0.5傪傕偮摿惈偲側偭偰偄傑偡丅廃攇悢摿惈偼僇乕僽偱帵偝傟傞傕偺偱偩偗偱偼側偄偙偲傪偍傏偊偰偍偄偰偔偩偝偄丅
 丂丂丂
丂丂丂 丂丂丂
丂丂丂