廃攇悢摿惈偺婎慴
攇宍傪暘夝偡傞
娙扨偵愢柧偡傞偨傔偵丄巹偨偪偑娤嶡偡傞夋憸傪俆亊俆僺僋僙儖偲偟偰榖傪恑傔傑偡丅
偼偠傔偵丄偙偺夋憸偺拞怱晹偺墶曽岦偩偗偵拲栚偟偰丄偦偺僺僋僙儖抣傪僾儘僢僩偟偰傒傑偡偲僈僞 僈僞偟偨攇偑弌棃偁偑傝傑偡丅偙偺攇偼廃婜偑摨偠偱偁傞傛偆側傕偺乮廃婜娭悢偲尵偄傑偡乯偱偁傟偽僼乕儕僄媺悢偲尵偆幃偱帵偝傟丄嶰妏娭悢乮sin攇傗cos攇乯偺崌惉偱弌棃忋偑傞偙偲偑抦傜傟偰偄傑偡丅偟偐偟丄夋憸偺傛偆側僈僞僈僞偟偨攇傗嬮宍攇偑1屄偩偗屒棫偟偰偄傞傛偆側攇偼丄廃婜揑偵曄壔 偟偰偄側偄偺偱僼乕儕僄媺悢偼巊梡偱偒偢僼乕儕僄曄姺傪巊傢側偗傟偽側傜側偔側傞偦偆偱偡丅
僼乕儕僄曄姺傪娙扨偵弎傋傞偲丄夋憸偺傛偆側僈僞僈僞偟偨攇宍偺拞偵娷傑傟傞怓乆側廃攇悢偺攇偺怳暆乮攇偺崅偝乯傪挷傋傞曽朄偩偲巚偭偰偔偩偝偄丅
乮埵憡傕偁傞偺偱偡偑丄 偙偙偱偼徣棯偟傑偡丅乯
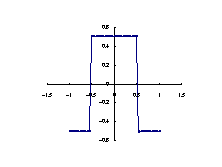
壓偺恾偼嬮宍攇傪僼乕儕僄媺悢偱寁嶼偟廃攇悢偺堎側傞攇傪帵偟偨傕偺偱偡丅
嬮宍攇偼嘆乣嘋偺廃攇悢偺攇偵暘夝偡傞偙偲偑偱偒丄斀懳偵嘆乣嘋偺攇宍傪崌惉偡傞偲嬮宍攇偵栠傝傑
偡丅嘆+嘇偺攇宍偵嘊傪壛偊偨偺偑嘆+嘇+嘊丄偦傟偵嘋傪壛偊偨偺偑嘆+嘇+嘊+嘋偺攇宍偱嬮宍攇偵嬤偯
偄偰偄傞偙偲偑傢偐傝傑偡丅
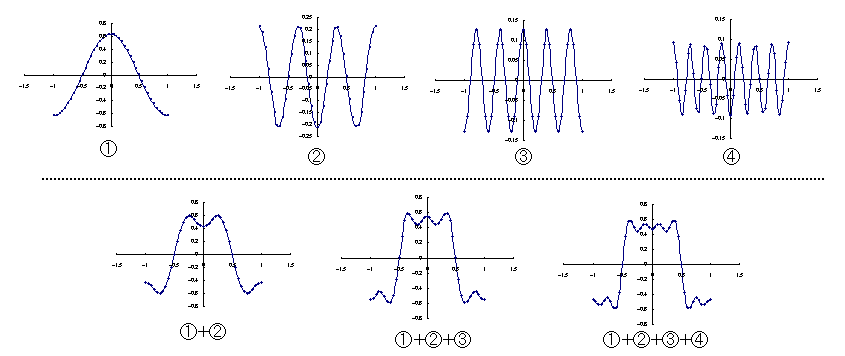
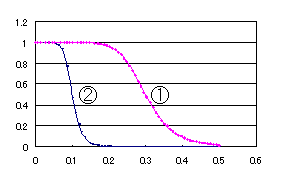
偙傟傜偺廃攇悢枅偺怳暆偲廃攇悢傪僌儔僼偵偟偨偺偑廃攇悢摿惈偱偁傝丄墶幉偵廃攇悢乮嬻娫廃攇悢乯
丄廲幉偵偼偦偺廃攇悢偺怳暆傪庢傝傑偡丅嘆偺摿惈偼崅廃攇偵側偭偰傕怳暆偺抣偑彫偝偔側傜偢丄嘇
偼崅廃攇偵側傞偵偮傟偰怳暆偑彊乆偵掅偔側偭偰偄偭偰偄傑偡丅偙偺嬋慄偐傜嘆偺傛偆側摿惈傪傕偮攇偼崅廃攇偵側偭偰傕怳暆偑彫偝偔側傜側偄偺偱丄崅廃攇惉暘乮嵶偐側攇乯傪偄偭傁偄娷偔傫偱偄傞攇偩偲尵偊傑偡丅嘇偼崅廃攇偺怳暆偑彊乆偵彫偝偔側偭偰偄傞偺偱丄掅廃攇偑懡偔娷傑傟偰偄傞攇偩偲夝庍偱偒傑偡丅
偱偼丄幚嵺偺廃攇悢摿惈偺寁嶼偺傗傝曽傪棟夝偟偰偄偒傑偡丅愭傎偳傕弎傋偨傛偆偵夋憸偺攇偼楢懕偱偼側偔僺僋僙儖娫妘偺抣傪帩偮偨傔僼乕儕僄媺悢偼巊偊偢僼乕儕僄曄姺偵傛傜側偗傟偽側傝傑偣傫丅
傑偨丄偙傟傜偺僼乕儕僄曄姺偼棧嶶僼乕儕僄曄姺乮DFT乯偱偍偙側偆偲偺偙偲偱偡偺偱偦偺曽朄傪愢柧偟傑偡丅
曽朄偼摿暿偵擄夝側寁嶼偱偼側偔幃偵抣傪偁偰偼傔偰寁嶼偡傟偽廃攇悢摿惈偑媮傑傝傑偡丅偳偆偟偰偙偺傛偆側幃偵側傞偺偐偼峫偊側偄偱寁嶼偺傒偟偰偔偩偝偄丅
 丂丂丂
丂丂丂 丂丂丂
丂丂丂



