核医学画像処理の基礎（１）

1次元・２次元画像

ＲＩやＣＴ、ＭＲなどのデジタル画像は６４×６４とか１２８×１２８、 ５１２×５１２のピクセルで表現された画面のなかで画像となって描出されて います。６４×６４の画像とは、縦横それぞれに６４個のピクセルをもつ四角の画面（合計６４×６４＝４０９６個のピクセル集合）であると言うことです。 この画面は縦横の画面であるため２次元画像とも呼ばれます。難しい言葉ではありません。

２次元画像とは私たちが一般に観察する画像のことです。

ならば、１次元画像とはなんでしょうか？スライス厚を決めるときに、何ピクセ ル（何センチ）に指定するか解析装置が聞いてきます。このとき１ピクセルのスライス厚と指定すると６４×６４個（４０９６個のピクセル）のピクセル中で１ピクセル分（横方向）が指定されたことになります。この画像は横に並んだ６４個のピクセルで構成される画像であるために１次元画像と表現されるのです。

この２次元や１次元画像の言葉を知っておくことは、画像解析（コンボルーシ ョン積分や空間周波数など）をするときに役立ちます。画像解析に利用される 計算は２次元で理解しようと思うと難しいのですが、最初に１次元で覚え、その後、２次元で応用できるようにすると難しい式もぼんやりと理解できるものです。


実空間と周波数空間

２次元画像や１次元画像については説明しました。今度は実空間や周波数空間の言葉を理解します。

実空間とは、私たちが普通に観察するピクセルの集まり での表された空間です。実空間なんて高尚な言葉を使うと難しく聞こえますが 普通の画像のことです。

周波数空間とは、普通の画像をフーリエ変換し周波数の空間に変換したものです。ここで周波数空間を詳細に説明すると訳が分からなくなるかもしれませんので止めます。はじめは実空間でフィルタや画像解析を覚え、その後に周波数 空間を理解すれば十分ですので実空間からいろいろ理解していきます。


フィルタ

平滑化フィルタやButterworthフィルタなどのなじみ深いフィルタがあります。 このフィルタの正体はなんなのでしょうか？よく１，２，１の９点平滑化フィ ルタ（スムージングフィルタとも言います）などと書かれた参考書をみること があります。

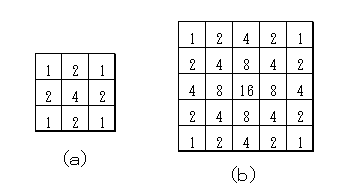
フィルタとは平面画面のそれぞれのピクセルに数値を入れたものです。分かり難いですか？最もなじみの深い９点スムージング（３×３マトリック）を例に して説明します。９点スムージングフィルタとは、３×３のマトリックスの画 面作り、それらの９個のピクセルに数値（整数）を入れます。その数値は下の 図に示す整数で、これがスムージングフィルタなのです。この数値の入れ方で フィルタの性質（特性）が変わります。下の図（ａ）は９点スムージングフィルタ（重み１，２，１）を示し、９個のピクセルに縦横のピクセル値が１，２， １の関係になるように整数をあてはめたものです。これが２５点（５×５ピク セル）になると（ｂ）のようなフィルタとなります。これも縦横の関係が１， ２，１になっています。
いまの説明は２次元なのですが、いろいろな計算方法（コンボルーション積分 やフーリエ変換など）を理解するときには１次元の１，２，１のフィルタも知 っておく必要があります。先の２次元、１次元画像とはで説明したように、横方向のピクセルを取り出せば１次元の１，２，１フィルタとなるのです。

このようにフィルタとは、縦横のマス目に整数（実数のものもある）を入れたものであると理解してください。

この整数の並び方でいろんなフィルタが出来あがります。どんな数字が入るかを説明するにはややこしい計算（？）が必要になりますので後ほど説明します。