再構成フィルタの種類
前頁でH(u)=|u|のフィルタがでてきました。このフィルタをRampフィルタと呼んでいます。これ以外に再構成フィルタにはShepp&LoganフィルタやChesler(Hann)フィルタなどがあることはご存知と思います。ここではこれらのフィルタについて簡単に説明します
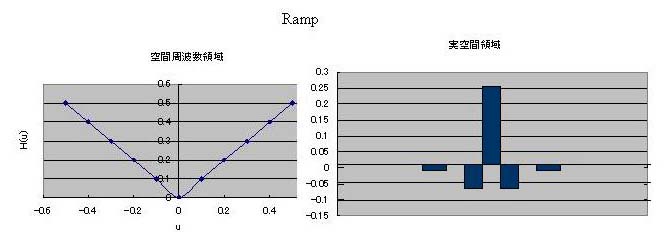
1)Rampフィルタ
Rampフィルタは空間周波数領域ではH(u)=|u|の特性となっています。この特性を逆フーリエ変換し実空間領域で表すと下のようになります。
g(ka)=1/4a2 (k=0のとき)
=−1/(πka)2 (k:奇数のとき)
=0 (k:偶数のとき)
ここでkはフィルタ中心を0としています。中心から離れるに従いk=±1、K=±2となっていきます。
具体的に説明しますと、aはサンプリング間隔ですので、ピクセル単位で示したらピクセルの最小単位は1ピクセルとなりますのでa=1ということになります。
ですから、フィルタの中心を0としましたからk=0(中心)でのg(ka)=1/4a2はg(中心)=1/4になります。
右方向に1ピクセル移動したところの値はk=1ですからこれは奇数となります。
したがって、上の(k:奇数のとき)の式g(ka)=−1/(πka)2は、g(1)=−1/(π×1×1)2=−1/(π)2=ー0.10132となります。
右方向に2ピクセル移動したところの値はk=2ですからこれは偶数になります。
したがって、上の(k:偶数のとき)の式g(ka)=0となっていますから、2ピクセル移動したときのg(2)=0となります。
右方向に3ピクセル移動したところの値はk=3ですからこれは奇数となります。
したがって、上の(k:奇数のとき)の式g(ka)=−1/(πka)2は、g(3)=−1/(π×3×1)2=−1/(π×3)2=ー0.0112となります。
同じように右方向、左方向へ移動したときのg(ka)を計算すれば実空間での特性が求まるわけです(下図参照)。
このフィルタは高周波を直線的に増加させていくフィルタであり、ナイキスト周波数で高周波成分をカットしているため雑音がのりやすい欠点があります。(再構成画像には雑音が含まれているのでそれにRampフィルタのuを掛けてしまうと雑音も増強されてしまいます。

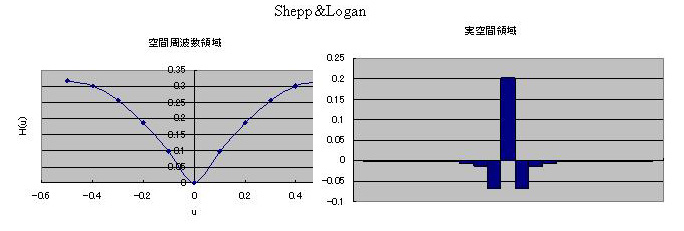
2.Shepp&Loganフィルタ
Shepp&LoganフィルタはRampフィルタの欠点でもある高周波成分による雑音を抑制したフィルタと言えます。
空間周波数領域では
H(u)=2um/π×|sin(πu/um)| (um:ナイキスト周波数)
実空間領域では
g(ka)=2/π2a2(1-4k2) (k=0、±1、±2・・・・・)
となるフィルタです。
ナイキスト周波数(最高周波数)は0.5ですのでum=0.5としてH(u)を計算させ、実空間ではRampと同じ計算をすれば下図が求まります。
これらのフィルタはどのように使われるのか?
このようにフィルタの概要は理解できたとおもいますが、実際にはどのような計算でこれらのフィルタが利用されてるのでしょうか?
これには2通りの計算があります。1)空間周波数領域で計算する方法と2)実空間座標で計算する方法があります。東芝社製の解析装置は実空間、他のメーカでは空間周波数領域で計算されてるようです。ではこれら2つの違いについて考えていきます。
1)空間周波数領域での計算
a)実際に収集した60枚の画像(プロジェクションデータ)をそれぞれフーリエ変換する。これをF(u)とします。
b)次に、ボケを補正する空間周波数領域での再構成フィルタH(u)を準備します。
c)ここで収集した画像F(u)と再構成フィルタH(u)を掛け合わせる。(F(u)×H(u))
2)実空間領域での計算
a)実際に収集した60枚の画像(プロジェクションデータ)のそれぞれの画像を準備する。
b)次に、実空間領域での再構成フィルタを準備する。
c)この画像同士のコンボルーション積分をおこなう。
簡単に述べれば以上のことにより、再構成フィルタで処理した60枚の画像ができあがることになります。