多方向からの逆投影

前頁では４方向からの逆投影によるボケについて考えてきました。ここでは実際の投影数（例えば６０方向）について考えてみます。

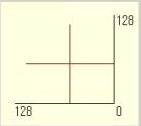
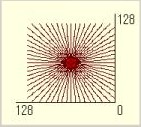
上の左図は４方向からの投影データを逆投影したものです。右図は６０方向からの逆投影のものです。本来は中心に像が現れなければならないのですが、単純に逆投影したのでは、逆投影数が増すほど中心やその周辺のボケが目立ってきます。これでは逆投影しても本来の像を得ることはできないのです。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

逆投影のボケはどのようになっているのか？

上の右図の中心部（赤のライン）をスキャンしその濃度（強度）変化を観察してみます。

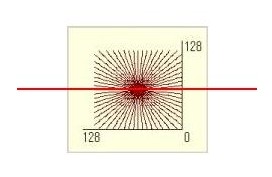
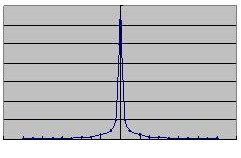
すると右図のようなプロファイルカーブができあがります。本来は中心のみに像ができあがるわけですから、この曲線と反対の形をしたカーブをフィルタとして使えば周りのボケている部分の像は加算されて消去されることがわかると思います。（再構成フィルタについて（１）で説明したのと同じ原理です）

すなわち、逆投影に用いるフィルタは下図のような形にすれば良いことになります。

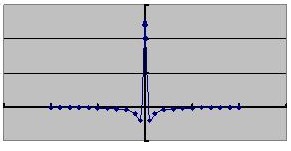
このような形をしたフィルタが再構成フィルタとなるのです。これを実空間（ピクセル単位で示す）で表すと下のようになります。

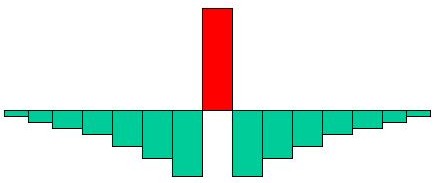
これを少し数学的に考えてみます

逆投影によるボケは、上のプロファイルカーブで示したようになることは理解できたと思います。
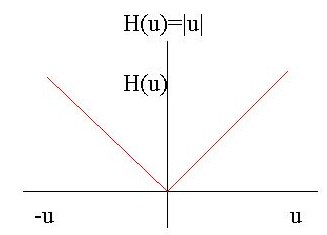
これを数学的に記述すると、「逆投影によるボケ距離に逆比例する」ことになります。おなじように周波数領域で考えるとボケ（振幅）は空間周波数(u)の増加とともに減少する１/uとなります。

ボケが１/uとなるならば、その逆数であるuを乗ずればボケはなくなります。

１/u 　×　u = 1

したがって、空間周波数領域では　u となるフィルタを使用すればボケはなくなるということです。