Excelによる離散フーリエ変換(3)

1次元の離散フーリエ変換おこないながら、離散フーリエ変換を理解します。

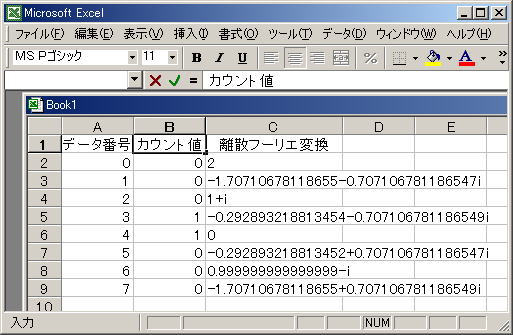
　0-0-0-1-1-0-0-0　と並んでいる値をサンプリングして離散フーリエ変換してみます。

0

0

0

1

1

0

0

0

　　　　　　　　　　　　　　　　　　

　　　　　　　

Ｅｘｃｅｌの分析ツール（フーリエ変換）を用いて、Ｃ行に離散フーリエ変換した値（複素数）を表示させます。

データ番号とカウント値の関係は、↓のグラフとして表す事ができます。

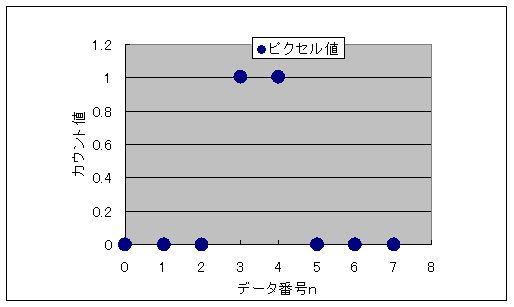
しかし、Ｅｘｃｅｌの分析ツールより求めた↑の離散フーリエ変換値は周波数空間での表示ですから、横軸はデータ（ピクセル）番号ではなくて空間周波数として示さなければなりません。

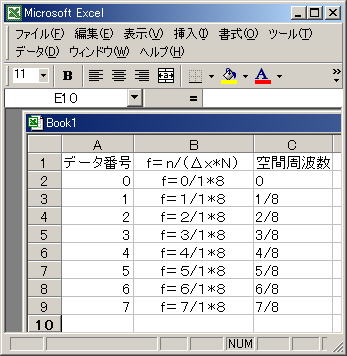
　　　　　　　　データ（ピクセル）番号ｎを空間周波数として表すには　ｆ　＝　n/（Δｘ*Ｎ）　の式を使用して変換します。

例えば、データ番号n=2を空間周波数とするには　ｆ　＝　2/（1*8）＝2/8　サイクル/ピクセルとなります。（サンプリング間隔はΔｘ＝１となります）
　ここで　ｆ　は　空間周波数、ｎはデータ（ピクセル）番号、　Ｎは全部のデータ個数、Δｘはサンプリングの間隔を表しています。
　　　　　

データ（ピクセル）番号　0の時のｆはｆ＝0/（1*8）＝0サイクル/ピクセル、１の時はｆ＝1/（1*8）＝1/8、２の時はｆ＝2/（1*8）＝2/8・・・・・・・・・・・・・・・・・
n=４の時はｆ＝4/（1*8）＝4/8＝0.5サイクル/ピクセル（ナイキスト周波数）となるので、4/8＝0.5サイクル/ピクセル以上のｆ＝5/8、6/8、7/8の周波数成分は3/8、2/8、1/8サイクル/ピクセルの負の周波数成分であることに注意しなければなりません。　　　　　　

以上のことから、データ番号が空間周波数に変換できましたので、横軸にはこの値を使用します。　（※　ｆ　＝　n/（Δｘ*Ｎ）｝　　

次は、縦軸ですが、離散フーリエ変換した値は複素数（a+bi)の形で計算されていました。この複素数を縦軸示す事はできませんので
違う形に変えます。

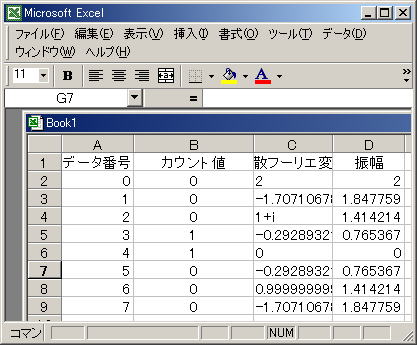
振幅値に変えてみます。a+biの振幅は√a2+b2　で示されました。（√はa2+b2全体にかかっています）

Ｅｘｃｅｌでは、＝ＩＭＡＢＳ（　）で計算できますので↓に計算例を示します。

*重要

ここで重要な公式があります。離散フーリエ変換した値にサンプリングした間隔（サンプリング周期）Δｘ　を乗じないとフーリエ変換値にはなりません。

　　　　　　　　　離散フーリエ変換値　Ｇｎ　　　　フーリエ変換値　Ｇ（ｆｎ）　とすると　　　　Ｇ（ｆｎ）＝Δｘ*Ｇｎ

ここではサンプリング間隔は１ピクセルなのでΔｘ＝１でよいのですが、サンプリングの間隔がｍｍとかsecで示されているときには、Ｇ（ｆｎ）＝Δｘ*Ｇｎの関係を忘れないようにしなければなりません。(サンプリング間隔が0.02ｍｍの時にはΔｘ＝0.02としてＧ（ｆｎ）＝Δｘ*Ｇｎ＝0.02*Ｇｎとします。）

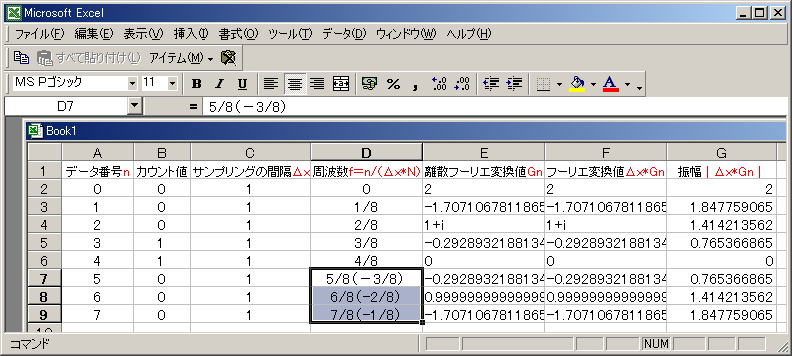
↑の結果より、周波数と振幅の関係をプロットすればフーリエ変換をおこなった結果となります。

周波数0.5以上は存在しませんから、グラフには表示しないようにします。