Excelによる離散フーリエ変換(2)

離散フーリエ変換を考える際に必要となる事項について記述します。

実空間と周波数空間の横軸の関係（ピクセル単位でサンプリングしたときとmm単位でサンプリングしたときの周波数について）

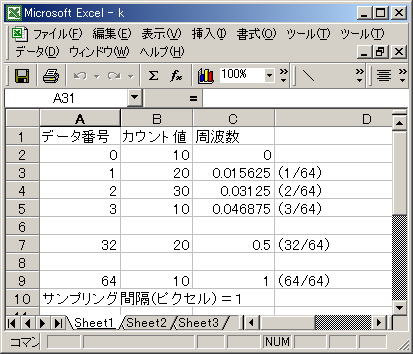
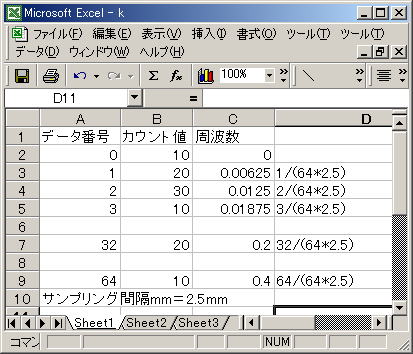
＊グラフ上とExcel表左はピクセル単位でサンプリングしたときの周波数を示しています。

＊グラフ下とExcel表右はｍｍ単位でサンプリングしたときの周波数を示しています。

データのサンプリング

実空間と周波数空間

*上のデータから離散的にデータを取得する事をサンプリングと呼んでいます。

*データ取得間隔（Δｔ）をサンプリング周期といいます。（画像は１ピクセル単位で画像データを取得しますので、サンプリング周期は１となります）

Δｔサンプリング周期の逆数を、サンプリング周波数と呼びます。（サンプリング周波数＝1/Δｔ）

サンプリング周期（Δｔ）でサンプリングされた離散的データから求めたフーリエ変換は、周波数軸上で周期1/（Δｔ）の周期関数になります。
　　　　　　　　　　　　　　　　　　　　　　　　　　　(右上グラフ参照）
注意：「周期1/（Δｔ）の周期関数になります」　画像の場合、サンプリングしているのは１ピクセル単位なので、周波数軸上の単位はサイクル/ピクセルとなるので、　　　　　1/（Δｔ）の周期関数とは1/1＝１サイクル/ピクセルの周期関数になることである。

DFTとフーリエ変換の関係

　　　　*DFTの結果F（DFT）からフーリエ変換F（ｆ）の結果に変換するには、F（ｆ）＝Δｔ×F（DFT）とする。

　　　　*<sup>振幅スペクトルも｜F(t)｜＝Δｔ×｜F（DFT）｜の関係となる。

　　　　*パワースペクトルとは｜F(ｔ)｜の２乗のこと</sup>

DFT式の係数1/Nの意味と振幅スペクトル

　　　*DFTを求める式には　F（DFT）＝1/NΣｆ（ｘ）・・・・との　F（DFT）＝Σｆ（ｘ）・・・・・の２つの表示がある。
　　　　　
　　　　　　　　F（DFT）＝1/NΣｆ（ｘ）を使用したときには、振幅スペクトルは^{｜F(t)｜＝N×Δｔ×｜F（DFT）｜}

　　　　　　F（DFT）＝Σｆ（ｘ）を使用したときには、振幅スペクトルは^{｜F(t)｜＝Δｔ×｜F（DFT）｜}
　　　　　　
　　　　　　　　　　　　これで、どちらの式を使用しても振幅スペクトルは同じ値になる。

　　　　　　　　　（離散逆フーリエの際には、F（DFT）＝Σｆ（ｘ）