統計の話（２）・・・・・平均値と標準偏差について

１．母集団と標本の平均値について

　前のページで、標本から得られた平均値（ｘバー）と標準偏差（ｓ）を母集団の平均値（μ）と標準偏差（δ）としてしまえと書きました。
なぜそのように考えるのかを記述します。


ここで仮定として次のように考えます。

仮定１）
母集団は５であるとします。採ってくる標本は２とします。Ｚ−scoreで使用される標本数は２よりは多いとおもわれますが、このような仮定で考えれば、全正常脳の人の数は５名であり、そこらら無作為に２名の患者さんをとりだして、脳の平均値と標準偏差を求めたことと同じ条件になりまます。

仮定２）
脳のピクセル当たりのカウントはそれだけか知りませんが、ここでは５名の脳のカウントを２０、４０、６０、８０、１０とします。
この母集団から２名のカウントを取り出してきます。


以上の仮定のもとに母集団と標本の平均値と標準偏差について考えてみます。

１）　母集団の平均値と標準偏差を計算します。

　　　　　　　　　　　　　　　　　平均値（μ）＝（２０＋４０＋６０＋８０＋１００）/５　＝　６０

　　　　標準偏差（δ）＝ＳＱＲ（（２０−６０）＾２＋（４０−６０）＾２＋（６０−６０）＾２＋（８０−６０）＾２＋（１００−６０）＾２）/５）　＝　２８．２８　　　

　　となります。

２）　２名分の標本を取り出します。

　　　１０通りの取り出しパターンがあります。

　　　　２０と４０の２つを取り出したときを（２０、４０）とします。次のパターンは（２０、６０）、次は（２０と８０）・・・・・・・（８０、１００）となります。
　　　　下に全ての取り出しパターンを記述します。


　　　　（２０、４０）　（２０、６０）　（２０、８０）　（２０、１００）　（４０、６０）　（４０、８０）　（４０、１００）　（６０、８０）　（６０、１００）　（８０、１００）


　　　ここで２人のカウントから標準脳の平均値と標準偏差を決めているのですから組み合わせのパターンでの平均を調べてみます。

　　　　　　　　　　　　　　　　　　　（２０、４０）の時の平均は（２０＋４０）/２　＝３０
　　　　　　　　　　　　　　　　　　　（２０、６０）　　　　　　　　　（２０＋６０）/２　＝４０
　　　　　　　　　　　　　　　　　　　（２０、８０）　　　　　　　　　（２０＋８０）/２　＝５０
　　　　　　　　　　　　　　　　　　　（２０、１００）　　　　　　　　（２０＋１００）/２＝６０　
　　　　　　　　　　　　　　　　　　　（４０、６０）　　　　　　　　　（４０＋６０）/２　＝５０　　　　　　・・・・・・・平均値の組
　　　　　　　　　　　　　　　　　　　（４０、８０）　　　　　　　　　（４０＋８０）/２　＝６０
　　　　　　　　　　　　　　　　　　　（４０、１００）　　　　　　　　（４０＋１００）/２＝７０
　　　　　　　　　　　　　　　　　　　（６０、８０）　　　　　　　　　（６０＋８０）/２　＝７０
　　　　　　　　　　　　　　　　　　　（６０、１００）　　　　　　　　（６０＋１００）/２＝８０　
　　　　　　　　　　　　　　　　　　　（８０、１００）　　　　　　　　（８０＋１００）/２＝９０
　　　　　　　　　　　　　　　　　　　

このようにして得られた平均は３０〜９０までの値をとり、取り出されたペアーにより平均値も変わってきてしまい、母集団平均６０とは違った値になります。じゃあもし偶然に（２０、４０）が取り出されたら平均は３０になってしまい母集団の平均６０とはかけ離れた値になってしまって困ったことになります。

ここで終わらないでもう少し奥深くみていきます。

もう一度２つの標本の平均値を記述します。
（３０、４０、５０、６０、５０、６０、７０、７０、８０、９０）となっています。先の説明では、偶然に（２０、４０）の組み合わせが選ばれて、母集団の平均値６０とはかけ離れているので困ったと記述しました。これは、取り出された組み合わせの平均が３０になったのは偶然の結果で必ずそうなるとは限りません。

ここで、分布と確率を考えてみましょう。


２つの取り出しかたは１０組ありました。どの組み合わせが取り出されるかは不明です。いまは平均値を考えていますから、取り出される組の平均値の分布をしらべてみれば、平均値の出かたの分布がわかります。この平均値の分布の中から、私たちは１組を選ぶのですから分布を知ることが重要になります。


上の平均値の組のなかで、３０となるのは１つです。４０も１つです。５０は２つあります。６０は２つ、７０も２つ、８０は１つ、９０も１つです。
全部で１０個のありましたから、この１０個から平均値が３０となる取り出され方は１/１０です。４０となるのも１/１０、５０となるのは２/１０
６０は２/１０、７０も２/１０、８０となるのは１/１０、９０も１/１０となります。

その分布を示します。
　
　　　　　　　　　　　　　　　　　　　　


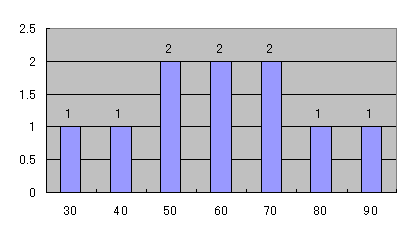
この結果から、平均値が３０となる確率は１/１０で全体からみれば１０％となります。しかし、平均値６０となる確立は２/１０（２０％）となり
ますから、母集団の平均値６０と同じ値を取ってくる確率は２/１０となり、平均値３０が選ばれる確率より高くなっています。

いまは、６０のみを考えましたが、母集団の平均値６０に近い値（５０、６０、７０）が取り出される確率を考えると　２/１０＋２/１０＋２/１０　＝
６/１０（６０％）が取り出される確率となります。

したがって、無作為に取り出される２つのサンプルの平均値の６０％は、母集団の平均値に近い値となりますから、確率からみても平均値が３０や４０、８０、９０の２つのサンプルが取り出されることはまれであると考えられます。

また、この分布から平均値（ｓ）を計算してみます。

　　　　　　　　｛（３０＋４０＋（５０×２）＋（６０×２）＋（７０×２）＋８０＋９０）｝/１０　＝６００/１０＝６０

となり、母集団の平均値（μ）＝６０と標本から求めた平均値の分布の平均とは一致しています。
このようなことから


　　　　　　　母集団の平均値は（μ）標本から取り出された平均値（ｓ）としてしまおうと考えているのでしょう。