理論は理解しないでML-EMをおぼえましょう
ML-EM法??参考書には期待値とか確率変数、ポアソン分布などの言葉が使われ、私にとっては意味不明の内容がでてきます。この再構成法の理論を把握することは必要なのですが、理論から入っていくと実際の計算を理解するまでには長い道のりがあり挫折してしまいます。
ですからここでは、理論なしに式を丸覚えして、ML-EM法はどのような方法であるのかをはじめに理解して、その後から理論を学びたいとおもっています。
まずは、なにも知らないことを前提にして説明していきます。
最尤推定ー期待値最大アルゴリズム?
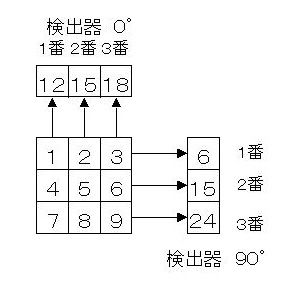
被写体を3×3マトリックスで、その中のカウントが1,2,3,4,5,6,7,8,9となっている被写体を検出器0°方向と検出器90°方向で収集したとします。吸収もなく、検出器にすべて正確に測定されるとすると、0°方向の検出器1番のカウントは縦列の1,4,7の総和12が計測されます。おなじように2番は15・・・・となります。
また、90°方向の検出器1番はマトリックスの横列の1,2,3の 総和6 が計測されます。

しかし、SPECT収集するときには3×3マトリックスの中身はわかりません。私たちにわかるのは、検出器( 0°)と検出器( 90°)方向の収集データの値のみです。
すると上の図は下のようになります。
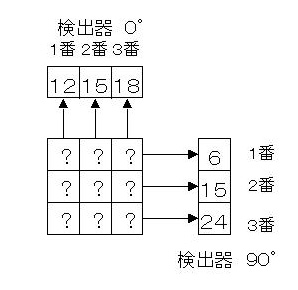
ML-EMとは、検出器の角度方向の収集データから、3×3マトリックスの箱の?の値を推定することです。最尤(さいゆう)推定との言葉があるように、最もら確からしい3×3マトリックスの中の?の値を数学的に決めてやろうとしているだけです。
数式を無視して理解します。
この方法に使用する数式は参考書によくでていますが以下のような数式です。数式の意味は理解しないで、最初はそのまま使ってみます。
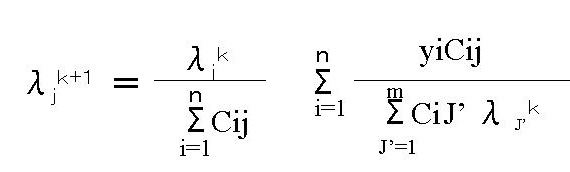
この数式をみると”あぁ〜”もう止めた!と思ってしまいます。難しい記号が使ってあるから複雑そうにみえてきます。もっと簡単に書きなおせばよいのかもしれません。こんな数式で収集データから3×3マトリックスの箱の数値を決めるのだ!とくらいに理解しておいてください。
実際に計算して数式の意味を理解しましょう。
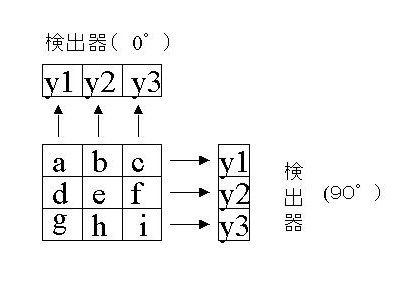
y1〜y3は検出器です。3×3マトリックスのaは0°方向の検出器y1に入ってきます。90°方向でもおなじ検出器に入ってきます。だから数式のyiは検出器に収集されたカウント値になります。
また、数式のλjkは3×3マトリックスのa〜iを意味しています。
数式のいたるところにでてくる Cij は3×3マトリックスのa〜iのカウントが検出器に収集される検出確率を示したものです。検出確率?この値はどうしたら求まるの???適当な値でかまいません。なぜなのかは後で述べます。
ですから、aのカウントが検出器で検出される確率も、bのカウントが検出器で検出される確率も、c〜iの検出確率は全て1として考えます。0.5でもかまいません。適当な値です。
ここまでで、数式のCij、yi、λjkはわかりました。
1) Cijは検出確率で全て1として考えます。
2) yiは検出器で収集されたカウントです。
3) λjkはa〜iのカウント値です。
ここから計算に入ります。
Cijの値は全て1にしましたからΣCijも計算できます。
yiもわかっている値ですから問題ありません。
でも、λjkはa〜iのカウント値であったのですが、このa〜iの値はわかっていませんからこまります。しかし、この計算でのa〜iははじめは正の値として考えようとの約束事がありますから、ここでは、最初の3×3の箱に入れるa〜iは1として計算をはじめます。
すると最初の図は下の図のようになります。
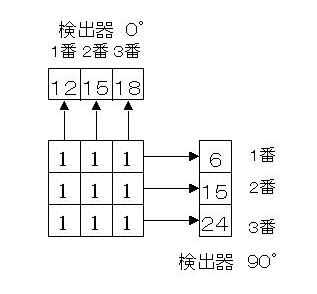
ここで疑問です。検出器0°の1番目のカウント値は12です。しかしこの12は3×3マトリックスの縦方向の総和として検出される値ですから、12になるわけがありません。縦の総和は(1+1+1=3)なのに12とはおかしい話です。
そこで、本来の3×3マトリクスの縦横列のそれぞれの総和(1+1+1=)3となる値を図の中にも書きます。そうすると上の図は下のようになります。
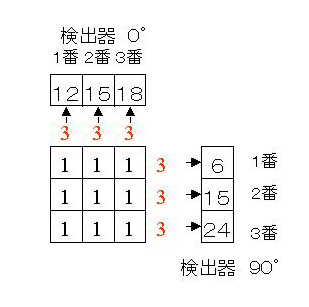
ここま理解すれば終わりに近いのです。
この1+1+1=3の3が数式のΣj’=1m(Cij’λj’k)
に相当するのです(検出確率を1としたとき)。
以上のことから、
3×3マトリックスaの計算は
1)λjkはaですので1
2)Σi=1m(Cji)は0°と90°方向での総和ですから、1+1=2となります。(Cijは全て1としてますからこのようになります。)
3)Σi=1m(yiCji)は(12×1+6×1)となります。(0°方向のyiは12、90°方向のyiは6で、Cjiは全て1ですからこのようになります。)
4)Σj’=1m(Cij’λj’k)=1×1+1×1+1×1=3
です。
実際に計算してみましょう!
[1].1回目の計算
1)3×3マトリックスの箱の中を1とします。

ここでCijは1としました。
aに初期値として1を入れています。
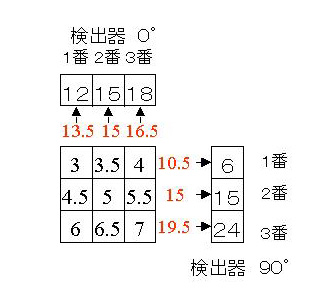
検出器1番目の計算からはじめます。その答えをa'とします。
a' = 1/(1+1)×((12×1/3)+(6×1/3))=1/2×(4+2)=3.0
これで終わりです。
b'も計算します。
b'=1/(1+1)×((15×1/3)+(6×1/3))=1/2×(5+2)=3.5
おなじようにc'〜i'まで計算します。
c'=1/(1+1)×((18×1/3)+(6×1/3))=4
d'=1/(1+1)×((12×1/3)+(15×1/3))=4.5
e'=1/(1+1)×((15×1/3)+(15×1/3))=5
f'=1/(1+1)×((18×1/3)+(15×1/3))=5.5
g'=1/(1+1)×((12×1/3)+(24×1/3))=6
h'=1/(1+1)×((15×1/3)+(24×1/3))=6.5
i'=1/(1+1)×((18×1/3)+(24×1/3))=7.0
すると最初の箱のa〜i=1は下のa'〜i'のようになります。
[2].2回目の計算
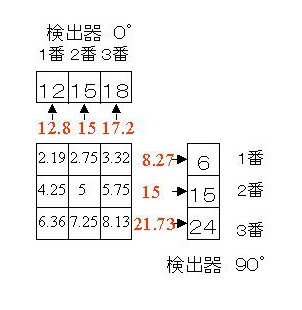
これも先ほどとおなじように計算します。次の答えをa''〜i''とします。
a''〜i''を計算します。
a''=3/(1+1)×((12×1/13.5)+(6×1/10.5))=2.19
b''=3.5/(1+1)×((15×1/15)+(6×1/10.5))=2.75
c''=4/(1+1)×((18×1/16.5)+(6×1/10.5))=3.32
d''=4.5/(1+1)×((12×1/13.5)+(15×1/15))=4.25
e''=5/(1+1)×((12×1/15)+(15×1/15))=5
i''=7/(1+1)×((18×1/16.5)+(24×1/19.5))=8.13
すると答えは下のようになります。
[3].3回目の計算
また同じ計算をします・・・・・この繰り返しの計算を26回繰り返すと下のような結果になります。
26回目の計算結果
この結果をみると、検出器0°の収集データと3×3マトリックスの縦列の総和(赤)、検出器90°方向の収集データと3×3マトリックスの横列の総和(赤)が等しくなっています。これが等しくなったところで計算を止め、マトリックスの中身をみます(ここでは四捨五入)。
1.46 → 1
1.99 → 2
2.54 → 3
3.96 → 4
4.99 → 5
6.04 → 6
6.57 → 7
8.01 → 8
9.42 → 9
すると、3×3マトリックスの箱の中身は
と解るのです。これがML-EMの概略です。