1.ばらつきを判定してみます
統計を考えるのに脳のカウントを例にして考えてきましたから、ここでも脳のカウントを例として、ばらつきについて考えます。
A病院で正常な3名の脳(大脳とします)のカウントを測定しました。そのカウントは 100 110 150 カウントになりました。
B病院でも同じように5名を測定したところ 90 100 110 120 130 カウントとなりました。
ばらつきはどちらがおおきいでしょう?
標準偏差や分散の計算方法を知っている方は容易に計算できますが、ここではなにもしらないと考えて分散と標準偏差について説明します。
どうしたらばらつきがわかるのでしょうか??
1)グラフを書いてみました。ばらつきの散布を表す散布図をかいてみます。
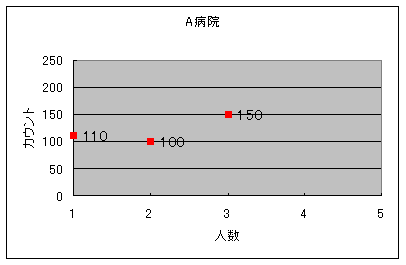
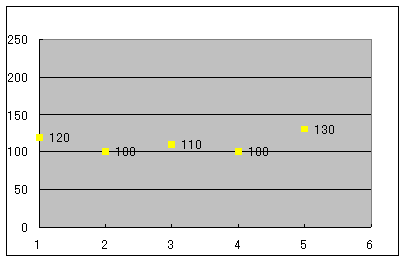
この散布図からどのようにしましょうか? 直感ではA病院の方がばらついているような気がするのですが・・・・・
2) カウントの幅をみてみます。A病院は最小のカウントは100で最高のカウントは150ですからこの差は150−100=50、となります。 B病院は90 が最低で130が最高カウントですので、差は130−90=40カウントとなりました。
だから、A病院の方がばらつきが多いと判定しました。
これでばらつきの判定はできたのでしょうか?
もし、ばらつきが少ないデータに一つ大きなデータが入ってきたらどうなるでしょうか?
3) B病院のデータを1人増やしたら、250カウントという値が求まったとしますと差は250−90=160となってしまいます。このデータは大きくかけ離れた データがきたために、5名ではばらつきがなかったものが1名の大きくかけ離れたデータがきたためにばらつきが大きくなってしまった例です。
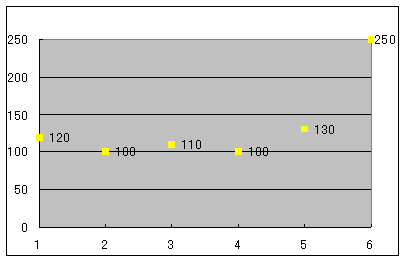
このように(最高値ー最低値)を求めたのではばらつきは判定できないことがわかります(統計では範囲と言っています)。