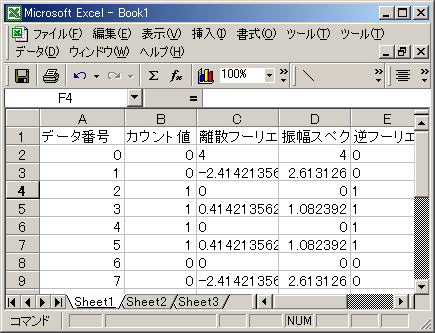
Excelによる逆離散フーリエ変換
0-0-0-1-1-0-0-0 と並んでいる値をExcelの分析ツール(フーリエ変換)を用いて逆離散フーリエ変換してみました。
結果は下のようになりました。

これを、画像処理の基礎の逆離散フーリエ変換で学んだ下の式で、Excelの分析ツールを使用しないで逆離散フーリエ変換の計算をしてみます。
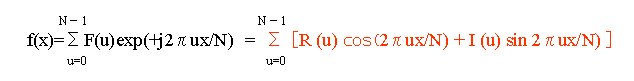
| u | フーリエ分析ツール使用 | 実際の計算値 | 実際の計算値のN=8倍 |
| 0 | 4 | 0.5 | 4 |
| 1 | -2.4142-0.9999i | -0.3017-0.125i | -2.4141-1.00i |
| 2 | 0 | 0.00001158+0.00001158i | 0.00009+0.00009i |
| 3 | 0.4142+0.9999i | 0.005174+0.1250i | 0.1431+1.0i |
| 4 | 0 | 0.000000007-0.0000231i | 0.00000008-0.00018i |
| 5 | 0.4142-1i | 0.00518-0.1249i | 0.4146-0.999i |
| 6 | 0 | -0.00003475+0.00003425i | -0.000278+0.00278i |
| 7 | -2.4142+1i | -0.3017+0.1248i | -2.4143+0.998i |
実際の計算値から算出されたR(u)とI(u)を用いて逆離散フーリエ変換してみます。
X=0のとき
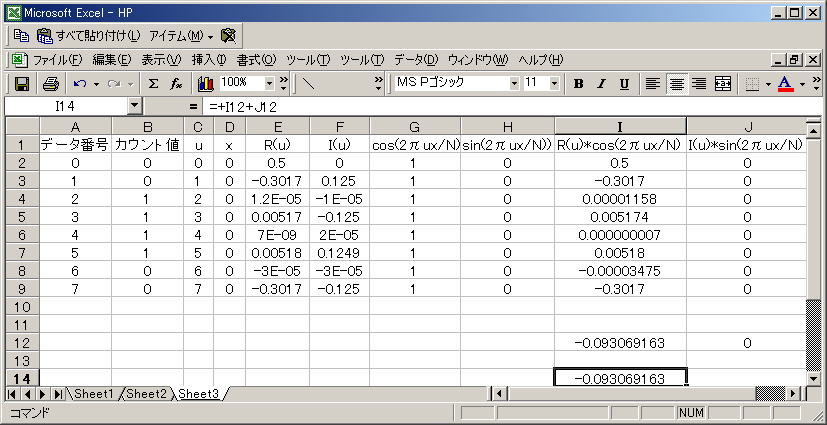
I14セルはx=0のときの離散逆フーリエ変換値(R(0)*cos(2πux/N)+I(0)*sin(2πux/N))はX=-0.093
となり、、ほぼX=0 の場所での値 0と 同じになり ます。
X=0のとき
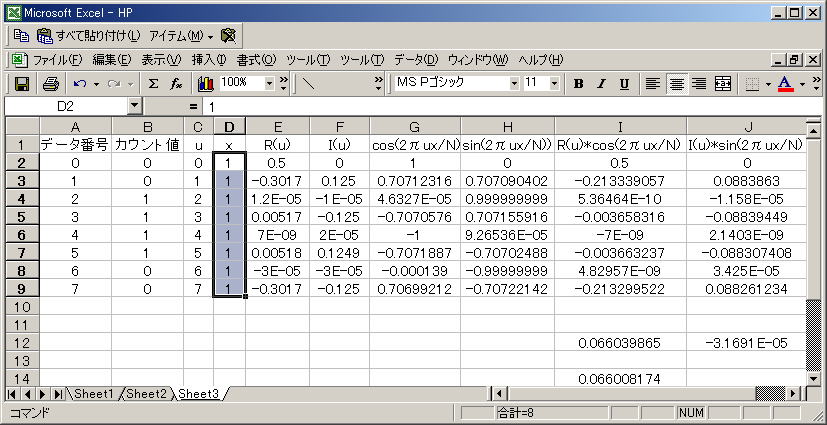
X=2のとき
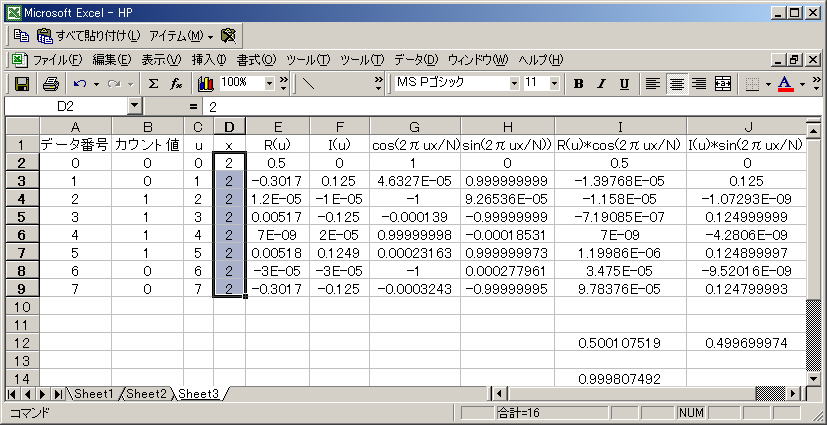
I14セルはx=2のときの離散逆フーリエ変換値(R(1)*cos(2πux/N)+I(1)*sin(2πux/N))はX=0.999 となり、、ほぼX=2 の場所での値 1と 同じになります。
同様にして X=3・・・・・7のときの離散逆フーリエ変換値を計算すれば元の値になっていることが確かめられます。
両者の値が違っています。
では、実際の計算例をN=8倍してみます。
| u | フーリエ分析ツール使用 | 実際の計算値 | 実際の計算値のN=8倍 |
| 0 | 4-0i | 0.5-0i | 4-0i |
| 1 | -2.4142-0.9999i | -0.3017-0.125i | -2.4141-1.00i |
すると、両者の計算値はほぼ同じになります。
これから、Excelによるフーリエ分析ツールによる値は F(u)=1/NΣf(x)・・・・ ではなく F(u)=Σf(x)・・・・となり
1/Nを乗じてない結果となっていることがわかります。